摘要: 本文采取多种方式(经文注释估算法、实地测量法、天文测算法)对佛经不同译本中常见的数值单位进行必要的换算工作。首先,我们发现佛经译本因传抄等原因存在明显的单位混用现象,特别是不同单位和“由旬”的混用。其次,我们认为将公牛挂轭行走一日之旅程的 11.2 千米称为“由旬”,是从古至今的错误。最后,本文再一次论证前文《小世界的整体结构》[6] 关于“由旬”换算的合理性,即一般人会因为不知道佛经译本存在单位混用现象而产生误解。
关键词:经文注释估算法、实地测量法、天文测算法、单位混用
重要声明
- 因本文的诸多结论建立在论文《小世界的整体结构》[6] 、《须弥山究竟在哪里?》[7] 和《四大部洲和小世界中心的须弥山》[5] 上,我们强烈建议读者首先依次完成上述文章的阅读。此外,本文后面的结论均建立在前面内容的分析上,请读者按照顺序阅读,理清系列文章所展示的逻辑论证路线,即证据链的形成过程,否则将产生断章取义式的曲解。
- 本文所解读的内容源于《起世经》、《起世因本经》及《佛说长阿含经》等原始佛教基本经典中所共有的相关内容,这些内容为全球大小乘佛教所共同承认。本文依然以《起世经》为主。
- 本文的观点有很多与传统不一样,也与很多网络流传的观点不一样。对任何一种佛学观点,本文不崇尚任何权威(包括所谓的佛学常识等),仅关注其是否满足经文描述的逻辑一致性以及是否存在符合现代科学观测的可验证性。我们有严格的证据表明,有很多所谓的佛学常识都是长期以来以讹传讹的谬误,毫无经典依据也无任何可验证性。事实归事实,信仰归信仰,本文力求只讨论可验证的事实,不愿讨论没有任何依据的纯粹信仰。
- 本文不采纳任何包括且不限于传说、传奇故事、未经主流科学界验证的实验结论和个别媒体采访事件等未经广泛证实的资料作为推理的依据。
- 本文力求,一切推理分析所依据的材料,所引用的佛典经文和相关科学知识及论文都是公开可查询、可验证、可核实,并且绝大多数参考材料均为主流科学界公认或有全球影响力的国家级权威机构确认。
- 本文的诸多结论建立在现代科学的研究成果上,请读者尊重现代科学 (包括各种生产技术及研究人员),不要做出任何非理性的反科学言论,以及各种完全无依据且无法验证的奇葩言论。
- 注意!本文并不构成对佛经神话世界存在性的直接证明,也不构成对佛经神话世界存在性的否定,只是阐述该问题存在某种匪夷所思的复杂性,并且在文中逐步展示这种复杂性。
- 包括本文在内的系列论文(文章)均已获得作品登记证书。著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明作者及出处。欢迎大家关注、讨论、分享和转发。
为什么我们认为可以对部分佛经进行基于现代科学观测的验证?
有以下几点理由:
(1) 在正确理解佛经的情况下,我们发现佛经中确实有很多内容可以验证,而可验证性才能确保解 读的正确性。
(2) 不是所有的佛经都阐述难以验证或完全无法验证的内容。
(3) 既然我们认为佛陀是伟大的智者,那么他显然知道一般人存在观测局限性,也必然会站在一般 人的角度并且以一般人的观测水平来描述事物,从而进行引导。否则,一切将毫无凭据,又何以取信于众? 我们认为佛陀显然具备这种因势利导的教学能力。
(4) 佛经《起世经卷第五·诸龙金翅鸟品第五》[29] 以“盲人摸象”来譬喻万物的“一体多面”性,而佛 陀所描述的事物中,有很多事物的“某一面”可以被不同的盲人触摸。如果说一般人 (凡夫) 是盲人,则很多事物显然存在可以“触摸”的“一面”,而这可以“触摸”的一面恰好构成了可以进行科学观测验证的基石。很多人误以为佛经的“盲人摸象”典故表明盲人一无是处,而我们却看到盲人恰有一处。因此,从佛经“盲人摸象”故事就已经表明佛陀所描述的事物“可以摸”,但只能摸到 “一面”。换言之,是佛经的典故表明可以“摸” (即进行科学观测验证)。
(5) 同时,我们也反复强调,经过科学观测验证的事物和佛经描述的对象存在“对应非等价”关系, 即因“一体多面性”导致的“对应非等价”关系,而这也是准确理解原始佛经最关键的地方。
综上所述,我们认为现代科学验证对部分经文必定有效。
1 译本的单位混用现象
在系列文章《小世界的整体结构》[6],我们换算出 1 由旬约为 4.42 米,并且在此后的文章(参考《须弥山究竟在哪里?》[7] 和《四大部洲和小世界中心的须弥山》[5]) 中论证了这个换算的合理性。在本文,我们将对佛经的其它度量单位进行研究并完成其中一部分的换算工作。
首先,佛经的单位包括两种,一是度量单位 (measuring unit),譬如,“由旬”、“俱卢奢”、“踰阇那”、“里”等。二是计数单位 (counting unit),譬如,千、万、百万、千万、亿、百亿、千万亿等。 在对佛经的数值描述进行换算的时候,我们需要同时考虑度量单位和计数单位是否正确。
其次,在近代人丁福保编写的《佛学大辞典》[13] 及佛学百科中,佛经单位“由旬” (Yojana)被认为与“踰阇那”相同,而佛经翻译中也常有将两者混用的现象。譬如,在《起世经》的译本中,“踰阇那”出现了 146 次,而在具有相同内容的《起世因本经》中却一次都没有出现,全部都换成了“由旬”。此外,我们经过文本搜索发现 70 卷的《正法念处经》其使用的度量单位除了一处出现“拘赊” 【参考经文“见有大河。名瞿陀婆利。其水清净。广一拘赊。长二百由旬。[9]”。此外,此处的“拘赊”极有可能是“俱卢奢”。】外,其余均为“由旬”(共 511 处)。因此,我们认为佛经描述山海的经文存在众多度量单位混用现象,常以“由旬”取代其它度量单位。
然而,本文的研究将表明,这两者无论是发音 (音译) 还是实际的估算值都相差甚远,不能等 同。强行等同只会造成一些夸张的表述,让人误以为佛经在描写奇幻的外星世界。
最后,根据度量单位几乎为音译的缘故,我们认为“踰阇那”、“踰缮那”、“瑜膳那”这三者相同,“由 旬”、“俞旬”、“由延”这三者相同,“俱卢奢”、“拘卢舍”、“俱嚧舍”、“拘卢奢”、“拘赊”这五者相同。
2 “里”的换算
我们发现部分佛经译文会出现度量单位“里”,譬如《正法念处经》的相关经文:
时阿修罗。欲破其军。于大海边。拔取大石。方四百里。或三百里。或二百里。或一百里。或一由旬。[8]
时婆罗门。以四千乘车。载众饮食。至大旷野。众人行路。欲施所须。见一佛塔。高二由旬。广五十里。[10]
在上面这两段经文中,“由旬”和“里”同时出现。由此可知,佛经在这里并没有使用“里”来换算 “由旬”,即无翻译的本地化 [20]。两者的共存意味着佛经中存在特有的度量单位“里”,其具体数值和我国古代的度量单位“里”无关。当然,是否佛经中所有的“里”都和古代的度量单位“里”无关,则需要具体问题具体分析。那么, 这个“里”究竟有多长呢?
2.1 经文换算法及初步验证
根据西晋三藏法师竺法护译的《琉璃王经》的相关经文:
又大海水。深广之量。三百三十六万里。[25]
及《起世经一卷第一·阎浮洲品第一》的经文:
诸比丘。其大海水最甚深处。深八万四千由旬。边广无量。[27]
可知,“三百三十六万里”与“八万四千由旬”相等,即 1 由旬为 336 ÷ 8.4 = 40 里。换言之,1 里为 1÷40 = 0.025 由旬,约 4.42÷40 = 0.1105 米。
因此,前面经文所描述的“四百里”为 0.1105 × 400 = 44.2 米、“三百里”为 0.1105 × 300 = 33.15 米、“二百里”为 0.1105 × 200 = 22.1 米、“一百里”为 0.1105 × 100 = 11.05 米,而“五十里”为 0.1105 × 50 = 5.525 米。由此可知,佛经的度量单位及数值描述在没有单位混用或其它干扰的情况下是严谨的。本节开头经文所描述的佛塔,即“见一佛塔。高二由旬。广五十里。[10]”,其高广比为 8:5。
2.2 “里”与“由旬”的混用
在前文中,我们曾分析过佛经度量单位的混用现象,特别是“由旬”与其它度量单位的混用 现象。本小节将进一步探讨“由旬”和“里”的混用现象。以下是西晋三藏法师竺法护翻译的《琉璃王经》的相关经文:
释氏豪姓。又亦多集。众出而御之。族党骁勇。强盛善射。射四十里者。射二十里者。十里者。七里者。任其本德。御飞破初。箭不虚发。能析一发。以为七分。去有里数射尽中之。寻声应弦。曾无遗漏。于是交战。射琉璃王军。穿幡折幢。裂盖摧杠。截辕韅摄。决铠带韅。绝弓弩弦。不害象马牛畜之命。射珥臂指环钏璎珞。而不中肌。翦除须发左右眉须发毛睫。亦不害体。琉璃怖骇。问臣下曰。敌去此几何。而箭所至伤毁若兹。答曰或四十里。二十里十里。近者七里。王闻加悸。不能自宁。[25]
这段经文描述了释迦族弓箭手的射程,并且表明释迦族的弓箭手“强盛善射”,令琉璃王深感恐惧 (“王闻加悸。不能自宁。)”。按照本节关于“里”的换算可知,“四十里”约 0.1105 × 40 = 4.42 米, 而“七里”约 0.1105 × 7 = 0.7735 米。这种距离作为古代弓箭的射程显然不符合常识。按照日常经验,一个三岁小孩用力抛掷手中的石块,其距离也不止 4.42 米。
如果我们将“里”换成“由旬”,则“四十由旬”约 4.42×40 = 176.8 米,而“七由旬”约 4.42×7 = 30.94 米。因古代弓箭的平均有效射程在 100 米左右,从 176.8 米到 30.94 米均属于古代弓箭正常合理的射程范围。此外,176.8米的射程在古代确实属于善射。
3 “俱卢奢”的换算
我们这里分别采取“经文注释估算法”、“实地测量法”以及“天文估算法”进行“俱卢奢”的估算。
3.1 经文注释估算法
首先,根据《阿毗达磨俱舍论卷第十二·分别世品第三之五》的相关经文:
三节为一指。世所极成。是故于颂中不别分别。二十四指横布为肘。竖积四肘为弓。谓寻。竖积五百弓为一俱卢舍。一俱卢舍许是从村至阿练若中间道量。[12]
可知,此处的 1 俱卢舍为 500 弓。根据前文的诸多分析可知,经文此处的“阎浮提人”即为我们熟 知的人类。又根据佛经在描述“阎浮提人”的寿命时采取 100 岁【“阎浮提人。寿命百年。”[28]】作为描述值,以及 2015 年世界百岁 老人人口统计 [1] 中百岁老人所占比例为 6.2/100,000 可推知,佛陀使用某种极大覆盖值作为定值方式。延续这种定值方式,我们假设一个极高的 2 米为地球人类身高的极大覆盖值。因此 1 肘的 长度约为 2.0÷3.5 ≈ 0.5714 米,1 弓约 2.286 米,而此处定义的 1 俱卢舍约为 2.286×500 = 1143 米。
其次,根据《起世经》对“俱卢奢”的长度定义有关的经文注释:
诸比丘。阎浮提人。身长三肘半。衣广中七肘。上下三肘半。[28]
一俱嚧舍(四肘名一弓千弓名一俱嚧舍)。[31]
以及前面分析的 1 弓 (4 肘) 约 2.286 米。此处的 1,000 弓为 1 俱卢奢,因此 1 俱卢奢约为 2.0 ÷ 3.5 × 4 × 1000 ≈ 2286 米。通过对比可知,其值为前面《阿毗达磨俱舍论》相关注释所估算值的 2 倍。
那么,为什么会出现两种不同的情况呢?我们且看《阿毗达磨大毗婆沙论卷第一百三十六·大 种蕴第五中具见纳息第三之三》的相关经文:
二十四指节成一肘。四肘为一弓。去村五百弓。名阿练若处。从此已去名边远处。则五百弓成摩揭陀国一俱卢舍。成北方半俱卢舍。所以者何。摩揭陀国其地平正去村虽近而不闻声。北方高下远犹声及。是故北方俱卢舍大。[4]
由上面的这段经文可知,500 弓的俱卢舍为摩揭陀国的度量单位,而北方俱卢舍大,为 1000 弓。显然,《起世经》的经文注释使用的是古印度北方的俱卢舍 (1000弓)。至此,我们可以认为佛经存在 2 种“俱卢奢”,分别为 500弓约 1143 米的“摩揭陀国俱卢奢”和 1000 弓约 2286 米的“北方俱卢奢”。 那么,究竟哪一种更符合一般经文的定义呢?
3.2 实地测量法
根据《根本说一切有部百一羯磨卷第三·次明结界法》(唐三藏法师义净译)的相关注释:
然则那烂陀寺南向王舍城。有五俱卢舍。计其里数可一驿余耳。[11]
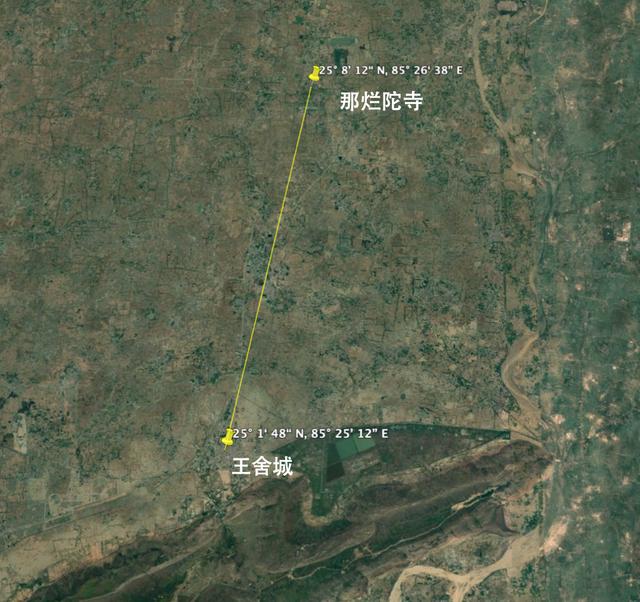
经文注释在这里提及那烂陀寺 [24] (Nalanda) 和王舍城 [21] (Rajgir) 之间的距离为 5 俱卢舍。根据现代考古学可知,那烂陀寺又作那兰陀寺、阿兰陀寺,意译为施无厌寺,全称那烂陀僧伽蓝。为古代中印度摩揭陀国首都王舍城北方之大寺院,其地即今拉查基尔 (Rajgir) 北方约十一公 里处之巴达加欧 (Baragaon)。而王舍城 (Rajgir),是印度次大陆的佛陀时代 (公元前 6-前 4 世 纪) 十六大国之一的摩揭陀国早期的都城,也是佛祖释迦牟尼长期居住修行的地方,佛陀逝世后, 在王舍城举行了第一次佛教结集,是佛教圣地之一。因此,根据两地相距约 11 公里以及经文注释的 5 俱卢舍可知,1 俱卢舍约为 11000 ÷ 5 = 2200 米。
此外,根据 Google Earth 专业软件的测量,那烂陀寺 [24] (Nalanda【遗址 [2] 地理坐标:25° 8’12“N, 85° 26‘38”E】) 和王舍城 [21] (Rajgir 【遗址园区 [3] 地理坐标:25° 1‘48“N, 85° 25’12”E】) 之间的距离为 12.05 千米 (详情见图1),可知 1 俱卢舍约为 12050 ÷ 5 = 2410 米。因两地之间的距离测量存在一定的定义模糊【究竟是从城市中心还是城门口开始测量,将导致若干千米的差距。】和测量误差,我们认为换算出的数值 2200~2410 米都是合理的范围,而这个范围也包含了《起世经》注释法所得到的 2286 米 (“北方俱卢舍”)。
最后,我们将前面不同的测算结果整理成表1。根据前面的分析可知,经文中的度量单位“俱卢奢”存在 500 弓的“摩揭陀国俱卢奢”和 1000 弓的“北方俱卢奢”,实地测量的结果则显然支持了 1000 弓的“北方俱卢奢” (也即《起世经》注释中的俱卢奢)。
综上所述,与“摩揭陀国俱卢奢”相比,我们认为“北方俱卢奢”更符合一般经文的定义。
3.3 天文测算法
我们且看《起世因本经》的相关描述:
日天宫殿。常行不息。六月北行。于一日中。渐移北向。六俱卢奢。未曾暂时离于日道。六月南行。亦一日中。渐移南向。六俱卢奢。不差日道。[26]
诸比丘。日天宫殿。六月已后。渐向南行。[26]
在文章《小世界的整体结构》[6],我们已经论证过佛陀知道地球是一个球体,而后续文章《须弥山究竟在哪里?》[7] 和《四大部洲和小世界中心的须弥山》[5] 的众多结论又“互相印证”了这一点。接下来,让我们看看上面这两段经文的含义。
上面这两段经文描述了佛陀解释冬天夜长昼短,而夏天昼长夜短的问题。佛经的表述是,太阳 (直射点) 在 6 个月时间内会逐渐向北移动,看上去每日向北偏移 6 俱卢奢的距离,实则轨道不变。而向北移动 6 个月后,就会开始为时 6 个月的向南移动,每日向南偏移 6 俱卢奢,太阳 (直射点) 的运行轨道不变。这些描述相当于叙述了南北回归线 [16] 的定义。回归线是太阳每年在地球上直射来回移动的分界线。根据现代地理学,南、北回归线指的是地球上南、北纬 23°26’ 的两条纬度圈。北纬 23°26’ 称为北回归线 [15],是阳光在地球上直射点的最北界线。南纬 23°26’ 称为南回归线 [17],是阳光在地球上直射点的最南界线。根据南北回归线 [16] 的夹角,即 23°26’×2=46.87°,和地球的半径 6371 千米,我们可以推算出南北回归线 [16] 的球面距离约为 2π × 6371 × 46.87 ÷ 360 = 5211.7 千米。太阳 (直射点) 6 个月 (半年) 走完,则每一天平均走 5211.7 ÷ (365 ÷ 2) = 28.557 千米,也就是经文中的“六俱卢奢”。换言之,1 俱卢奢约为 4,759.5 米,即 4,760 米。
对比《起世经》相关注释定义所估算出的 2286 米,天文测算法所得出的“天文俱卢奢”约为“北 方俱卢奢”的 4759.5 ÷ 2286 ≈ 2.082 倍。那么,这些估算可靠吗?
3.3 换算可靠性的初步验证
我们且看下面经文对云高度的描述:
诸比丘。世间有云。从地上升。在虚空中。或有至一俱卢奢住。或二或三俱卢奢住。乃至六七俱卢奢住。[30]
这一段佛经描述的是云层的高度,我们将不同测算方式得出的“摩揭陀国俱卢奢”、“北方俱卢 奢”和“天文俱卢奢”以及它们相关的“一俱卢奢住”、“二或三俱卢奢”及“六七俱卢奢”所对应的高度整理成表2。
根据现代气象学 [18],地球上的云层一般出现在大气的对流层 [19] (Troposphere),而对流层 的高度因纬度而不同,在低纬度地区平均高度为 17~18 千米,在中纬度地区平均为 10~12 千米,在高纬度地区平均为 8~9 千米,并且夏季高于冬季。此外,贝母云 [23] (Nacreous cloud) 作为一种色彩绚丽、薄而纤细的罕见云彩,可在高纬度地区 20~30 千米高空出现。因此,对比表2的相关数据,“摩揭陀国俱卢奢”所关联的数值偏低,而“北方俱卢奢”和“天文俱卢奢”所关联的数值均为地球上合理的范围。
综上可知,“俱卢奢”千米以上的换算数值和“由旬”的 4.42 米相去甚远,将“由旬”和“俱卢奢”混 淆将导致数值描述错误。此外,我们认为,无论是“摩揭陀国俱卢奢”、“北方俱卢奢”还是“天文俱卢奢”都有存在的价值,它们极可能在佛经的翻译和传抄过程中被逐渐混淆在一起。
4 “踰阇那”的换算
4.1 经文注释估算法
根据《根本说一切有部百一羯磨卷第三·次明结界法》(唐三藏法师义净译)的相关描述:
言瑜膳那者。既无正翻义。当东夏一驿可三十余里。旧云由旬者讹略。若准西国俗法。四俱卢舍为一瑜膳那。计一俱卢舍可有八里。即是当其三十二里。若准内教。八俱卢舍为一瑜膳那。一俱卢舍有五百弓。弓有一步数。准其步数才一里半余。将八倍之当十二里。此乃不充一驿。亲验当今西方瑜膳那。可有一驿故。今皆作一驿翻之。庶无远滞。然则那烂陀寺南向王舍城。有五俱卢舍。计其里数可一驿余耳。[11]
这段经文注释阐述了以下观点:
• 东夏一驿有 30 多里,旧时将这个距离称为“由旬”是错误 (讹) 的。
• 以西国俗法为准,则 4 俱卢舍为 1 踰阇那,1 俱卢舍为 8 里。以内教为准,则 8 俱卢舍为 1 踰阇那。按照 1 俱卢舍为 500 弓的算法,1 俱卢舍仅 1 里半,8 俱卢舍才 12 里,与一驿(30 多里) 相差甚远。
• 那烂陀寺南与王舍城之间有 5 俱卢舍,按照里数有一驿多(30 多里)。
根据前文的分析可知,那烂陀寺 [24] 和王舍城 [21] 之间的距离介于 11 千米和 12 千米之间,而近代人丁福保编写的《佛学大辞典》[13] 及佛学百科中,佛经单位“由旬”被认为是公牛挂轭行走一日 之旅程,大约七英里,即 11.2 公里(千米),也在这个范围内。经文注释表明,将这个距离称为“由旬”是错误的。由此可知,将公牛挂轭行走一日之旅程的 11.2 千米称为“由旬”,是从古至今的错误, 而唐三藏法师义净在经文注释中就明确指出这种错误。
此外,这段经文注释表明,以 500 弓为 1 俱卢舍,无论是 4 俱卢舍为“1 踰阇那”,还是 8 俱 卢舍为“1 踰阇那”都不足一驿。我们认为,这从侧面反映出 1000 弓为 1 俱卢舍的“北方俱卢奢”的 合理性。最后,我们如果以内教为准,按照 1000 弓为 1 俱卢舍、8 俱卢舍为 1 踰阇那,则“1 北方 踰阇那”为 2286 × 8 = 18288 米,约 18.29 千米。如果以“天文俱卢奢”为准,则“1 天文踰阇那”为 4760 × 8 = 38, 080 米,即 38.080 千米。
4.2 换算可靠性的初步验证
我们且看下段经文的注释:
若众生辈。离彼一百踰阇那住 (踰阇那者隋数四十里也)。[31]
佛经的翻译注释认为 1“踰阇那”为隋朝的四十里,而古代的“里”究竟有多长呢?根据相关资 料 [14] 可知,“里”起源于中国周代,当时一里为 18 引 =1800 尺,战国、秦汉一里约 415.8 米,后世实际长度历代不同。商周时期约为 406.8 米 (推算),秦汉时期约为 415.8 米 (标准取值),隋代 约为 531 米 (推算),唐代约为 454 米 (推算),清光绪 34 年约为 576 米,民国 1929 改为 500米, 与公制相对应。
而隋朝的 1 里为 531 米,因此 1“踰阇那”为 531 × 40 = 21240 米,即 21.24 千米。若以此处的 数值为标准,则与上面“北方踰阇那”估算出的 18.29 千米存在 (21.24 − 18.29) ÷ 21.24 ≈ 13.89% 的 误差。反之,若我们以 18.29 千米为标准,则可以推算出隋代的 1 里约为 18.29 ÷ 40 = 457.25 米。
因此,基于“北方俱卢奢”的“北方踰阇那”更符合一般经文的定义。
5 小结
结论 5.1 佛经翻译中存在度量单位混用的现象。譬如,“由旬”是最常见的和多个单位混合使用的度量单位。在梵文经文的多次传抄过程中,佛经度量单位“踰阇那”、“俱卢奢”、“里”都有可能和“由旬”互换且混用。因此,当出现“由旬”时,我们需要根据上下文来考虑是否为“踰阇那”,或其它度量单位,反之亦然。此外,需要特别注意将“踰阇那”误换成“由旬”的情况。在没有其他证据的情况下,我们依赖原经文的单位描述。
结论 5.2 佛经中出现的度量单位“里”,其中有一些,其具体数值和我国古代的度量单位“里”无关,更与现代的“一里”等于 500 米毫无关系。我们的分析表明 40 里为 1 由旬,即 1 里为 0.025 由 旬,约 0.1105 米。此外,佛经 (译本或传抄本) 中,“里”与“由旬”之间存在单位混用现象,有一些 “里”实则为“由旬”或其它度量单位。
结论 5.3 我们认为,“北方俱卢奢”为经文的标准“俱卢奢”。因此,在一般情况下,我们以“北方 俱卢奢”为准,即“1 俱卢奢”约 2,286 米。此外,基于天文测算法得出的“天文俱卢奢”,即 4,760 米, 也是经文单位混用现象下需要考虑的对象。在后文的分析中,我们将综合考虑这两种不同的“俱卢奢”。
结论 5.4 将公牛挂轭行走一日之旅程的 11.2 千米【约为那烂陀寺 [24] 和王舍城 [21] 之间的距离】称为“由旬”,是从古至今的错误,而唐三藏法师义净在经文注释中就明确指出这种错误。
结论 5.5 对于佛经的度量单位“踰阇那”,按照“内教法”及“北方俱卢奢”的定义,我们认为其值 (“北方踰阇那”) 约为 18,288 米。若按照“内教法”及“天文俱卢奢”,则为 38,080 米 (“天文踰阇那”)。在后文的分析中,我们将综合考虑这两种不同的“踰阇那”。
结论 5.6 我们换算出的 1 弓约为 2.286 米,1 肘约为 0.5714 米。
参考文献
[1] Wikipedia. Centenarian.
[2] Wikipedia. Nalanda.
[3] Wikipedia. Rajgir.
[4] 五百大阿罗汉等造唐三藏法师玄奘译. 阿毗达磨大毗婆沙论卷第一百三十六,大种蕴第五中具 见纳息第三之三. 乾隆大藏经.
[5] 今日头条:暗室的一缕光. 四大部洲和小世界中心的须弥山 (佛经不可思议的超时代性:三).
https://www.toutiao.com/i7068120577885700643/.
[6] 今日头条:暗室的一缕光. 小世界的整体结构 (佛经不可思议的超时代性:一). https:
//www.toutiao.com/i7068202893463224869/.
[7] 今日头条:暗室的一缕光. 须弥山究竟在哪里? (佛经不可思议的超时代性:二). https:
//www.toutiao.com/i7067520263922942498/.
[8] 元魏婆罗门瞿昙般若流支译. 正法念处经卷第二十,畜生品第五之三. 乾隆大藏经.
[9] 元魏婆罗门瞿昙般若流支译. 正法念处经卷第六十八,身念处品第七之五. 乾隆大藏经.
[10] 元魏婆罗门瞿昙般若流支译. 正法念处经卷第十八,畜生品第五之一. 乾隆大藏经.
[11] 唐三藏法师义净奉制译. 根本说一切有部百一羯磨卷第三,次明结界法. 乾隆大藏经.
[12] 尊者世亲造唐三藏法师玄奘奉诏译. 阿毗达磨俱舍论卷第十二,分别世品第三之五. 乾隆大藏 经.
[13] 日本真宗大谷派学僧织田得能. 佛学大辞典, page 3351. 中国书店出版社, 2011.
[14] 百度百科. 一里.
[15] 百度百科. 北回归线(太阳直射点在地球上最北的界线).
[16] 百度百科. 南北回归线.
[17] 百度百科. 南回归线(太阳每年在地球上直射来回移动的分界线).
[18] 百度百科. 大气层.
[19] 百度百科. 对流层.
[20] 百度百科. 本地化翻译.
[21] 百度百科. 王舍城.
[22] 百度百科. 由旬.
[23] 百度百科. 贝母云.
[24] 百度百科. 那烂陀寺.
[25] 西晋三藏法师竺法护译. 琉璃王经. 乾隆大藏经.
[26] 隋三藏法师达磨笈多等译. 起世因本经卷第十,最胜品第十二之二. 乾隆大藏经.
[27] 隋三藏法师阇那崛多等译. 起世经卷第一,阎浮洲品第一. 乾隆大藏经.
[28] 隋三藏法师阇那崛多等译. 起世经卷第七,三十三天品第八之二. 乾隆大藏经.
[29] 隋三藏法师阇那崛多等译. 起世经卷第五,诸龙金翅鸟品第五. 乾隆大藏经.
[30] 隋三藏法师阇那崛多等译. 起世经卷第八,三十三天品第八之三. 乾隆大藏经.
[31] 隋三藏法师阇那崛多等译. 起世经卷第四,地狱品第四之三. 乾隆大藏经.
End